
ตัวอย่าง การวิเคราะห์การถดถอยพหุคูณ (Multiple Regression Analysis)
ต้องการวิเคราะห์ว่ายอดขายสินค้า (TotalSale) ขึ้นอยู่กับปัจจัยอะไรบ้างดังต่อไปนี้ จำนวนพนักงานขาย (Saleman) ค่าโฆษณา (Advertising) และ ประสบการณ์ของผู้จัดการสาขา (Experience) โดยทดสอบที่ระดับนัยสำคัญทางสถิติ .05

ข้อมูล มีทั้งหมด 18 สาขา ดังนี้

ข้อตกลงเบื้องต้นของการวิเคราะห์การถดถอย
1.ขนาดกลุ่มตัวอย่าง (Sample Size) สถิติการวิเคราะห์การถดถอยพหุคูณ (Multiple Regression) เป็นสถิติอ้างอิงที่มีข้อตกลงเกี่ยวกับการแจกแจงของประชากร ดังนั้นขนาดกลุ่มตัวอย่างจึงมีความสำคัญในการทดสอบเพื่ออ้างอิงไปยังกลุ่ม ประชากร มีนักวิชาการหลายท่านได้เสนอแนวคิดการกำหนดขนาดกลุ่มตัวอย่างไว้ (รายละเอียดสามารถสืบค้นเพิ่มเติมได้)
2.ระดับความสัมพันธ์ระหว่างตัวแปรพยากรณ์ การวิเคราะห์การถดถอยพหุคูณนั้นตัวแปรที่นำมาใช้พยากรณ์ไม่ควรมีความสัมพันธ์กันสูงเกินไป (ไม่ควร > .80) เพราะหากมีความสัมพันธ์เข้าใกล้ 1.00 แสดงว่าตัวแปรนั้นเกือบจะเป็นตัวแปรเดียวกัน ซึ่งไม่เหมาะในการนำมาพยากรณ์พร้อมกัน สามารถใช้ PSPP ตรวจสอบได้โดยใช้คำสั่ง Bivariate Correlation ซึ่งได้ผลลัพธ์ดังนี้

3.ตัวแปรตามต้องมีการแจกแจงแบบปกติ (Normal Distribution) ตัวแปรต้องอยู่ในมาตรการวัดระดับ interval ratio ขึ้นไป และมีการแจกแจงแบบปกติ รายละเอียดการทดสอบสามารถเปิดดูได้ในบทความเรื่อง การทดสอบข้อตกลงเบื้องต้นของสถิติด้วย PSPP
ขั้นตอนการวิเคราะห์การถดถอยพหุคูณด้วยโปรแกรม PSPP
1.ตรวจสอบลักษณะความสัมพันธ์เบื้องต้น ด้วยแผนภาพ Scatter Plot ระหว่างตัวแปรพยากรณ์ (Saleman, Advertising, Experience) กับตัวแปรผลหรือตัวแปรตามตาม (TotalSale) โดยใช้โปรแกรม Spread Sheet ในโปรแกรม OpenOffice.org

2.หาค่าสถิติของตัวแปรต่างๆ ตามที่ต้องการโดยใช้คำสั่ง Descriptives

3.ตรวจสอบความสัมพันธ์ของตัวแปร โดยใช้คำสั่ง Bivariate Correlation พบว่าตัวแปรตาม (TotalSale) มีความสัมพันธ์กับตัวแปรพยากรณ์แต่ละตัว (Saleman, Advertising, Experience) อย่างมีนัยสำคัญทางสถิติ

4.หาความสัมพันธ์ระหว่างตัวแปรเพื่อการพยากรณ์ ด้วยคำสั่ง Linear Regression ได้ผลลัพธ์ดังนี้

5.นำตัวแปรพยากรณ์ จำนวนพนักงานขาย (Saleman) เข้าสมการถดถอยอีกครั้ง ได้ผลลัพธ์ดังนี้

สรุปตารางวิเคราะห์การถดถอยพหุคูณ
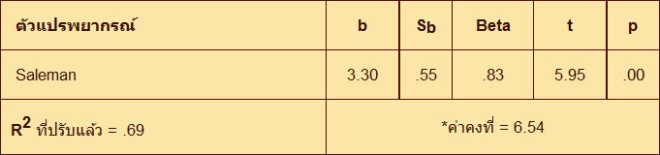
R2 คือสัมประสิทธิ์การทำนายหรือสัมประสิทธิ์การตัดสินใจ (Determination Coefficient) คำนวณจากค่าสัมประสิทธิ์สหสัมพันธ์ (Correlation Coefficient) ยกกำลังสอง
*ค่าคงที่ คือค่าที่เส้นถดถอย (regression line) ตัดกับแกน y
ผลการวิเคราะห์การถดถอยพหุคูณ พบว่ามีตัวแปรพยากรณ์เพียงตัวเดียวที่มีประสิทธิภาพการพยากรณ์ได้ 69% คือ Saleman (จำนวนพนักงานขาย) จึงมีลักษณะเช่นเดียวกับการวิเคราะห์การถดถอยอย่างง่าย (Simple Regression) โดยสมการการถดถอยพหุคูณจะเป็นดังนี้
y = ค่าคงที่ + b(x1) + b(x2) + ……………+ b(xn)
y คือตัวแปรผลหรือตัวแปรตาม (dependent variable)
x คือตัวแปรพยากรณ์หรือตัวแปรต้น (independent variable)
b คือค่าความชัน (slope) ของเส้นถดถอย ซึ่งแสดงอัตราการเปลี่ยนของ y เมื่อ x เปลี่ยนแปลงไปหนึ่งหน่วย
ในกรณีนี้ถ้ากำหนดให้จำนวนพนักงานขาย (Saleman) = 20 คน จะสามารถพยากรณ์ยอดขายได้ดังนี้
ยอดขาย = 6.54+3.30(20) = 72.54 ล้านบาท
การตรวจสอบลักษณะของเส้นถดถอย (regression line) และลักษณะความสัมพันธ์เบื้องต้นของตัวแปรด้วยโปรแกรม OpenStat
โปรแกรม OpenStat มีคำสั่ง X Versus Y Plot ใช้สำหรับตรวจสอบลักษณะของเส้นถดถอย และลักษณะความสัมพันธ์เบื้องต้นของตัวแปร 2 ตัว นอกจากนั้นยังมีส่วนของ Options ที่ผู้วิเคราะห์สามารถกำหนดรายละเอียดของการแสดงผลของแผนภูมิได้

เมื่อนำข้อมูลของตัวแปรพยากรณ์ Saleman (จำนวนพนักงานขาย) กับตัวแปรผล TotalSale (ยอดขายสินค้า) มาตรวจสอบลักษณะของเส้นถดถอยด้วยคำสั่ง X Versus Y Plot

ในการพยากรณ์ของตัวแปรผล y (Totalsale) ที่เกิดจากการกำหนดค่าของตัวแปรพยากรณ์ x (Saleman) จากสมการถดถอยที่ได้จะมีความแม่นยำเพียงใดนั้นขึ้นอยู่กับข้อมูลที่รวบรวมมา ว่ามีการกระจายไปจากเส้นถดถอยมากน้อยเพียงใด ถ้าค่าของตัวแปรผลแต่ละค่าแตกต่างไปจากค่าที่อยู่บนเส้นถดถอยมาก การพยากรณ์ค่าของตัวแปรผลโดยใช้เส้นถดถอยนี้ก็จะเกิดความคลาดเคลื่อนมาก ในขณะเดียวกันถ้าค่าของตัวแปรผลแต่ละค่าอยู่บนเส้นถดถอย หรือแตกต่างไปจากค่าที่อยู่บนเส้นถดถอยเพียงเล็กน้อย การพยากรณ์ค่าของตัวแปรผลโดยใช้เส้นถดถอยนี้ก็จะถูกต้องมากขึ้น สถิติที่ใช้วัดการกระจายของข้อมูลรอบๆเส้นถดถอย เรียกว่าความคลาดเคลื่อนมาตรฐานในการพยากรณ์ (Standard Error of Estimate : SEE) ซึ่งก็คือส่วนเบี่ยงเบนมาตรฐานของข้อมูลรอบเส้นถดถอย ถ้า SEE มีค่าน้อยแสดงว่ามีการถดถอยน้อย ถ้า SEE มีค่ามากแสดงว่ามีการถดถอยมาก
ไม่มีความคิดเห็น:
แสดงความคิดเห็น